Introduction
A random walk with restart is a stochastic process to traverse a graph, resulting in a probability distribution over the vertices corresponding to the likelihood those vertices are visited. This probability can be interpreted as the relatedness between nodes in the graph. The random walk starts with an initial distribution over the nodes in the graph, propagating the distribution to adjacent vertices proportionally, until convergence.
Formula
Let T be the transition matrix of the graph, with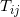 
being the probability of reaching entity 
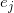from entity 
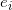,which can be computed as follows::
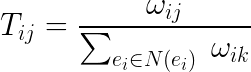
in which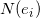 
is the set of entities directly reachable from 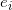, and 
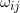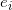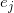is the weight of the edge between and ,defined as the number of their co-occurrences in the knowledge base.
Let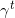 
be the probability distribution at iteration t, then 
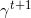is computed as follows:
where λ is restart probability S is the preference vector (in order to avoid the issues caused
by sinks and guarantee convergence).
Formally, the random walk model can be modeled as:
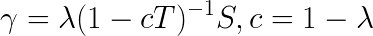
Demo
import random
import numpy as np
def EntityRWS(G, restart_rate, root, max_step):
'''
Computer Simulate Random Walk with Restart
'''
rank = dict()
rank = {x:0 for x in G.keys()}
rank[root] = 1.0
for k in range(max_step):
tmp = {x:0 for x in G.keys()}
total={x:0 for x in G.keys()}
for i, ri in G.items():
tmp[root]+=rank[i]*restart_rate
total[i]=sum(ri.values())
for j, wij in ri.items():
tmp[j] += rank[i] * (wij/total[i])*(1-restart_rate)
rank = tmp
print('iter: ' + str(k) + "\t"+str(rank))
return rank
def Cal_feature(G,restart_rate,root):
'''
Use Formula,however always "Singular Matrix Error"
'''
probability=np.zeros(shape=(len(G),len(G)))
total={x:0 for x in G.keys()}
Name=[x for x in G.keys()]
for i, ri in G.items():
total[i]=sum(ri.values())
for j, wij in ri.items():
probability[Name.index(i)][Name.index(j)]=wij/total[i]
c=1-restart_rate
#for k in range(len(G)):
#probability[k][k]=0.5;
print(probability)
new_probability=1-c*probability
print(new_probability)
S=[]
for x in G.keys():
if x == root:
S.append(1)
else:
S.append(0)
new_probability=abs(np.linalg.inv(new_probability))
print(new_probability)
print(S)
feature=restart_rate*np.dot(new_probability,S)
return feature
if __name__ == '__main__' :
G={"A":{"a1":1},
"B":{"b1":1,"b2":1},
"C":{"c1":1,"c2":1,"c3":1},
"a1":{"A":1,"d1":1},
"b1":{"B":1,"d2":1},
"b2":{"B":1},
"c1":{"C":1,"d1":1,"d2":1,"d3":1},
"c2":{"C":1,"d3":1},
"c3":{"C":1,"d3":1},
"d1":{"a1":1,"c1":1},
"d2":{"b1":1,"c1":1},
"d3":{"c1":1,"c2":1,"c3":1}}
G1={"A":{"B":1,},
"B":{"A":1,"C":2},
"C":{"B":2}}
print(EntityRWS(G1, 0.5, 'A', 100))
print(Cal_feature(G1,0.5,'A'))